Course Project, CS460, Fall 2021-22

On Federated Learning and Possible Improvements

Saswat Das
1811138 | saswat.das@niser.ac.in | School of Mathematical Sciences, NISER, HBNI
Suraj Ku. Patel
1811163 | suraj.kpatel@niser.ac.in | School of Physical Sciences, NISER, HBNI

Project Github Repository

1. Project Proposal (6 Sept 2021)

Introduction

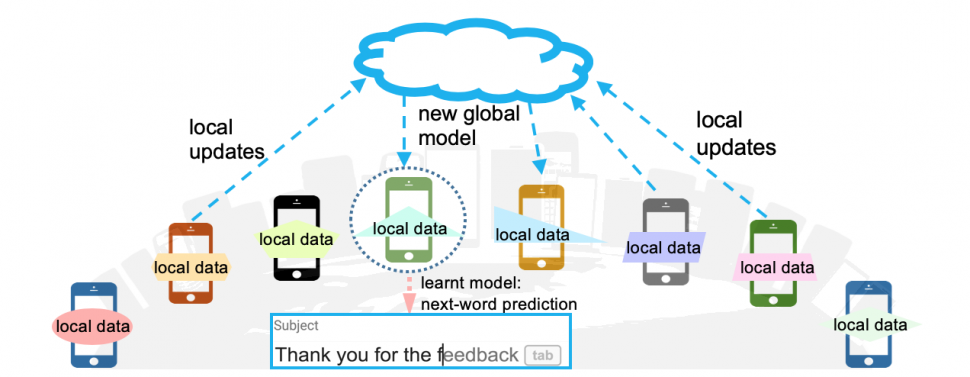
Federated Learning Schematic

 

Federated learning (abbreviated as FL) refers to the practice of conducting machine learning based on several users' data by having each user, given an initial global model by a central server, locally train a model on their local devices, then communicate their locally trained model to the central server, following which each user's local model is aggregated at the central server with that of others, and used to update the global model.

This is in contrast to centralised learning, where the users' data would have been sent to the central server, and a model would have been trained on all that collected data in one central server.

Advantages?

Quite some!

  1. The user's personal data never leaves their local device, thus ensuring a healthy measure of privacy;
  2. Can possibly incorporate nuances of each user's local model by a suitable aggregation technique/algorithm to provide better, more nuanced learning.
Concerns/Areas of Possible Improvement

What we intend to do - a brief sketch

Then we will see how said tweaks work in terms of these metrics and report any observed improvements/changes (fingers crossed).

Midway Targets

Work Division

  1. Coding/Privacy based considerations - Joint task, will divide up coding of different components fluidly as needed.
  2. Data analysis and visualisation - Suraj
  3. Mathematics, formulae, proofs - Saswat
  4. Report writing and project website maintenance - Joint task

Expected Results

Relevant Papers

Project Presentation Slides

2. Project Midway

Literature Review

Some of the most important papers we referred to are listed below.

  1. McMahan et al
  2. Wei et al
  3. Konečný et al
  4. Extra: Ji et al

Techniques Used/Explored

Experiments and Observations

We implemented FedAvg from scratch in Python, with a 0.25 static sampling rate, with anywhere between 3 to 5 (or more) rounds of calling for training from sampled (w.r.t. the uniform distribution) clients, with local training involving multiple linear regression implemented via Stochastic Gradient Descent on a synthetically generated dataset for about 500 clients, with static subsampling (contrast with dynamic subsampling).

The generated datasets, generated around a pre-chosen/generated "true weights vector" (we chose the dimension of these weight vectors to be 7) (e.g. \([1, 2, 4, 3, 5, 6, 1.2]\) ), are mostly IID as we focused more on implementing a model atop that.

As we are using regression here, we use, for a particular instance, average training/testing error per data point as a metric of a deployment’s accuracy, and simply measure the time taken by running it on Google Colab and compare them as a rough measure of how quick each is, and implement centralised learning to serve as a baseline for our exploration of these FL paradigms.

We then tried the above listed techniques, sometimes standalone or in conjunction with each other as follows.

  1. Centralised Learning (As a Baseline)

    For centralised learning, we simply gathered and flattened the list of all local datasets into a cumulative list of all datapoints, and ran SGD on it for 100 epochs.
    Time Taken \(\approx 268-270\) seconds.
    Average Training Error for Centralised Learning on SGD \(\approx 3.2472\times 10^{-29}\).
    Average Testing Error for Centralised Learning on SGD \(\approx 3.2154 \times 10^{-29}\).

  2. Vanilla FederatedAveraging/FedAvg

    We then ran vanilla FedAvg with static sampling of clients at a rate of 0.25 of the client population per round of training on the above mentioned local datasets, with 100 epochs per round of local training. Number of rounds, \(T=5\) .
    Time taken \(\approx 362\) seconds.
    Average Training Error for Vanilla FedAvg on SGD \(\approx 2.5331\times 10^{-18}\) .
    Average Testing Error for Vanilla FedAvg on SGD \(\approx 2.6021\times 10^{-18}\) .

    1. Noising before Aggregation (From Wei et al)

      Adds Gaussian noise to appropriately clipped weights from each user. Motivation: To stop attacks involving reconstruction of raw data/private information from naïve uploading of weight vectors/matrices. Optionally adds downlink DP, but we felt it was unnecessary.

      We ran FedAvg with static sampling of clients at a rate of 0.25 per round of training, clipping the locally generated weight vectors to gain bounds (defining upper bound of the norm of a weight vector as \(C =1.01\times\max(w_i)\) , where \(w -\) weight vector, for the sake of computing the sensitivity of queries for the weight vectors, then adding Gaussian noise calibrated to \(C,\varepsilon,\delta\) to each weight ( \(\varepsilon=70,\delta=0.1\) ) with 100 epochs per round of local training. Number of rounds, \(T=5\) .
      Time taken \(\approx 349\) seconds (which makes it about as fast as vanilla FedAvg).
      Average Training Error for NbA FedAvg on SGD \(\approx 7.2562\times 10^{-7}\) .
      Average Testing Error for NbA FedAvg on SGD \(\approx 6.6740\times10^{-7}\) .

  3. NbAFL with Random Mask

    We use the same setup as for the above NbAFL implementation, but with a layer of uniformly chosen random masks, excluding \(\approx s=0.25\) of the weights, prior to uploading by a client. Seems to consistently outperform base NbAFL in terms of accuracy, also reduces communication overhead!
    Time taken \(\approx 356\) seconds.
    Average Training Error \(\approx 0.006601\).
    Average Testing Error \(\approx 0.007577\).

  4. NbAFL with Probabilistic Binarisation

    We again use the same setup and parameters as our vanilla NbAFL implementation, but with probabilistic binarisation implemented atop it.
    Time taken \(\approx 356\) seconds.
    Average Training Error \(\approx 0.021241\) .
    Average Testing Error \(\approx 0.019635\)

  5. NbAFL with Dynamic Sampling

    We again adopt the same setup as that for our vanilla NbAFL implementation, but instead of static sampling of clients, we sample clients with an initial rate of \(0.25\) , which decays by a factor of \(\frac 1{\exp(\beta t)}\) , where \(t =\) number of rounds elapsed. We take \(\beta=0.05\) .
    Time taken \(\approx 334\) seconds.
    (Saves on time and no. of communication rounds!)
    Average Training Error \(\approx 0.010684\) .
    Average Testing Error \(\approx 0.010908\) .

The following table summarises the parameters used for and the results of our experiments (to be fair, we had to fiddle with a fair of different values for parameters and variations in algorithms to fix these for now)

Local Learning Rate, \(\alpha = 0.01\) ; No. of local iterations for SGD \(=100\) , No. of clients \(=500\)
Name of Model T Client Sampling Rate \(\varepsilon\) \(\delta\) Training Error Testing Error Time Taken (sec) Other Parameters
Centralised SGD - - - - \(3.2472\times 10^{-29}\) \(3.2154 \times 10^{-29}\) 268 - 270 -
Vanilla FedAvg 5 0.25 - - \(2.5331\times 10^{-18}\) \(2.6021\times 10^{-18}\) 362 -
NbAFL 5 0.25 70 0.01 \(7.2562\times 10^{-7}\) \(6.6740\times10^{-7}\) 349 -
NbAFL w/ Random Mask 5 0.25 70 0.01 0.006601 0.007577 356 \(s=0.25\)
NbAFL w/ Prob. Bin. 5 0.25 70 0.01 0.021241 0.019635 356 -
NbAFL w/ Dyn. Samp. 5 0.25 70 0.01 0.010684 0.010908 334 \(\beta=0.05\)

Note that the errors happen to be quite small compared to the weight vectors' magnitude, with a maximum being in the neighbourhood of 1% error to "true" weight vector (norm/coordinates) ratio, roughly.

Suggested Tweaks and Possible Improvements to Try Out to Extend the Baselines

We may tentatively try implementing the above FL models for more complex local training algorithms (viz. ConvNets using FEMNIST), but this is secondary/optional.

Here is the link to the .ipynb file containing the midway version of our code.

Some Midway References

  1. H. B. McMahan, E. Moore, D. Ramage, and B. A. y Arcas, “Communication-efficient learning of deep networks from decentralized data,”, 2016.
  2. K. Wei, J. Li, M. Ding, C. Ma, H. H. Yang, F. Farokhi, S. Jin, T. Q. S. Quek, and H. V. Poor, “Federated learning with differential privacy: Algorithms and performance analysis,” IEEE Transactions on Information Forensics and Security, 2020.
  3. J. Konecny, H. B. McMahan, F. X. Yu, P. Richt ́arik, A. T. Suresh, and D. Bacon, “Federated learning: Strategies for improving communication efficiency,” CoRR, vol. abs/1610.05492, 2016.
  4. S. Ji, W. Jiang, A. Walid, and X. Li, “Dynamic sampling and selective masking for communication-efficient federated learning,” CoRR, vol. abs/2003.09603, 2020.

Midway Presentation Slides

(Kindly Exclude The Title and Bibliography Slides from the Slide Count)

 

3. Final Project Presentation/Extension of Baselines

 

    Since the midway, we did a number of things, the most notable of which are as follows.

  • Created a federated learning code framework from scratch to transfer our work from one that employs local learning via linear regression on a randomly generated dataset to one that employs DNNs (implemented on Tensorflow) to classify digits in MNIST (randomly shuffled and distributed across clients).

  • Tried out various approaches and tweaks to some existing paradigms/models.

  • Designed "Adaptive Sampling" an improvement to Dynamic Sampling, with penalisation of the sampling decay coefficient for increase in errors.

  • Designed a fully decentralised P2P approach to FL (in contrast to the recent P2P models proposed that involve a level of temporary centralisation).

  • Designed an approach involving clustering (of clients) in silos and simultaneously training a silo-specific model and a general model via FL.

 

Specifications of our new framework

Dataset:

MNIST (training data shuffled and distributed unequally at random among 100 clients)

Local Training:

Via a DNN, defined and compiled with Tensorflow.

  • Input Layer: Flatten Layer.

  • Hidden Layers: 32 units and 512 units* (later ditched for speed) with ReLU activation.

  • Dropout Layer* (rate = 0.2): Before the \(2^\text{nd}\) Hidden Layer (later ditched)

  • Output Layer: 10 units with Softmax activation.

  • Batch Normalisation: Before every hidden and output layer

In a nutshell, due to time and computing power constraints, we ended up using a DNN with a flatten layer, a hidden layer with 32 units with ReLU activation, followed by an output layer with 10 units with softmax activation, not to mention the batch normalisation layers before the hidden and output layer. As we shall soon see, we found that this was sufficient to give a high degree of accuracy on MNIST.

Federated Averaging was implemented similarly as for our older framework, as per the original paper on Federated Averaging by McMahan et al.

A salient feature of our framework is that it is flexible enough to be used for any Tensorflow based neural network (at least ones that are created using keras.sequential) and for any dataset that is fed into such an NN.

Baselines

N.B. For testing, we initialised the same server model (i.e. we started training with a weight vector that was common for every run, for example, a weight vector with all 0s for each "coordinate" in the vector) for each run of each model, for a fair comparison.

Given the conception of the new code framework with the DNN on MNIST, we re-ran some of the relevant baselines using it, and we got the following results. Please note that the provided figures/graphs are representative, as in they are just a few from the many runs of each model/algorithm.

Centralised Learning
Which simply is training the DNN using all of the MNIST training data in one place, and precisely what any federated learning algorithm should aspire to match, or at least approach, in terms of accuracy.
Test Accuracy: 96.52% (Pretty nice!)

image

Vanilla FedAveraging

Which, as mentioned earlier, is simply an implementation of McMahan et al's model with aggregation via FederatedAvg. Note that here in each round of communication, a fixed proportion of the total number of clients are asked for local updates, which in the language of client sampling is called static sampling.
Number of Communication Rounds: 50
Test Accuracy: 94.21% (Not bad at all!)

image

FedAveraging with Dynamic Sampling

For a proper recaptitulation of what Dynamic Sampling does, refer to our prior discussion regarding Ji et al in the Midway section. But in a nutshell, what it does is reduce the number of clients sampled per round w.r.t. a decay coefficient \(\beta\) and the initial client sampling rate (i.e. by multiplying \(\frac 1{\exp(-\beta t)}\) to the initial sampling rate).

Decay Coeff. \(\beta\) : 0.05
Initial Sampling Rate : 0.25
Test Accuracy: 93.7%
Number of Rounds: 50

image

Note that dynamic sampling decreases the number of clients per round independent of the change of accuracy per round.


The problem? This can slow down convergence and error rectification, or even occasionally and briefly lead to consecutive increases in error because aggregation of several client weights leads to a good aggregate weights estimate, but instead, the number of clients is continually decreasing here with the naive approach that decreasing the number of clients per round would decrease the volume of communication. Okay, that is true, but especially in a short term manner. In the long term, slow error rectification will lead to the model requiring a larger number of rounds of communication, which incurs both a time cost and communication cost in that way. But we can see that the thinking behind this paradigm is not without merit, we got a really good accuracy for substantially less clients' involvement vis-a-vis the vanilla case. But can we couple the reduction of the number of clients with faster convergence in a way that we are fine having the initial decay coefficient (which is positively correlated to how fast the decay occurs) as long as the error does not increase beyond a previously attained error value, at which point we would want to slow down the decay and make sure to involve more clients than in the last round to mitigate the amount of error and bring the amount of accuracy eventually to the highest previously attained accuracy beyond which it fell off. This is precisely the motivation behind us introducing adaptive sampling.

More clients involved \(\implies\) Better averaging \(\implies\) Less error.

I. Adaptive Sampling

That is, we keep successively penalising the decay coefficient for any fall in accuracy, while retaining the previous index, so as to increase the number of clients for the next round and slow the decay in the sampling rate down, and restore the decay coefficient when accuracy reaches the previous high.

The pseudocode for adaptive sampling is as follows.

image

 

Note : \(n_i\) is the number of datapoints possessed by the client corresponding to \(\Omega_t^i\) , and \(n\) is the total of all \(n_i\) ’s for each \(\Omega_t^i\in L\) .

Also, note that \((\gamma)\) is just a parameter we introduced in case we needed to tune the penalisation of the decay coefficient, and we kept it equal to 1 to start off with, and as it turned out, that worked just fine, so we kept it at 1.

We again ran several rounds of experiments for adaptive sampling and some representative results, with similar parameters as for the previous representative run for dynamic sampling, are as follows:

Initial Decay Coeff. \(\beta\) : 0.05
Initial Sampling Rate : 0.25
Gamma \((\gamma)\) : 1
Test Accuracy: 94.16%
Rounds of Communication: 20

(It would have risen as accuracy fell in the last step; it had an accuracy of 94.59% after round 19, but since we only specified 20 rounds of communication, it stalled at that.)

 

 

 

 

 

 

 

 

 

What immediately jumps out at us upon viewing this graph is that 1. it seems to lead to smoother convergence, sans any of the jaggedness as for dynamic sampling; and 2. it leads to convergence within lesser rounds of communication, albeit with marginally more clients per round on average being involved than dynamic sampling (owing to the penalisation of the decay coefficient at times along with stalling of the counter variable whenever accuracy drops), and knowing/assuming that the server calls on clients for communication round wise and clients in each round upload their local weights nearly simultaneously, lesser number of rounds implies lesser time taken for this entire exercise of federated learning.

II. Fully Decentralised P2P FL Learning:

Motivation:

In federated learning, the server aggregates the weight vector of the devices to make a new model, which implies a significant degree of centralisation, which in turn creates a single entity for an adversary to attack or track communications to; alternatively, sending weights to a central server might not be desirable in certain contexts for the sake of privacy.

In addition, traditional federated learning does not address its implementation for P2P networks, which has much potential given the advent of decentralisation to the extent that we see nowadays, and that of smart contracts and decentralised apps (dapps). Naturally, this has been a recent field of inquiry as far as federated learning is concerned.

So, we decided to formulate a model for peer-to-peer learning where local training is done for all the peers involved in a round of training, and then after exchanging local weights among themselves, each device independently performs aggregation via FedAveraging (which in itself is not exactly an expensive task), and can compare the newly aggregated model with their existing ones to see what works best for them, and as a secondary consequence, guard against injection of illicit values by any malicious peer(s) (and we also gave quite some thought on how to nullify/penalise the malicious peer's influence or even remove them entirely in such an event).

Baselines for P2P Learning

To reiterate, federated learning in the context of P2P networks (i.e. sans a server) is a nascent field of study.


Some of the earliest models like BrainTorrent (2019), and that by Behera et al (JPMorgan Chase & Co., 2021) involve taking (i.e. randomly choosing/electing) a temporary "leader" peer node to act in the capacity of the server, thus inducing a level of centralization, and the peers having to accept the leader’s aggregation in good faith.


Others like FedP2P (2021) involve a model wherein a central server organizes clients into a P2P network after some bootstrapping is done at the server-end, and are not suitable for fully decentralized P2P networks.

Then there are models like IPLS (2021) involve a client acting as a central "leader/server" that assigns tasks to its peers, which resembles task delegation more than imploring devices to work on their own data and their own data only.

All of the serverless models we have come across involve making a peer a "temporary leader/server", and thus have a level of centralization, which brings privacy risks along with it. We aim to remove this aspect to obtain a completely decentralized FL paradigm for P2P networks.

Description of the Algorithm:

  1. A dapp or smart contract specifies an initial random model for all the devices in a round of communication/training.

  2. A device/peer may send a call for updates to all its peers, periodically or of its own volition.

  3. If a good enough proportion of peers agree, then they initialize with a common initial model (specified within the contract initially, else the last shared global model), and train local models. The last 2-3 "accepted" global models for a peer, if any, are stored locally.

  4. Each device calls for a number of those locally trained weights from a significant proportion (or all) of its peers and aggregates it.

  5. If the model performs better than its existing model, it keeps it (updates the local instance of dapp/smart contract accordingly), else ditches it.

Peers query for how many models ditched the new global model, if a majority do, then initialize the next round of training with the last viable one. (Defends the system against erroneous value injection.)

Experimental Results

In our experiments for our P2P federated learning mode, we simulated 100 peers/clients on the aforementioned framework on DNNs/MNIST, with a 0.25 client sampling rate. (Though, practically speaking, all this does is explore the case when 0.25 peers decide to participate in a round of training per round, though perhaps in a real life implementation, it may very well go beyond that, as peers shall seek to maximise the number of them that participate in a given round. 25% of clients chosen at random seemed to be a pretty good conservative estimate to us.)

Another caveat: we assume the absence of a malicious peer here, though should one be there, it cannot cause any damage due to each peer choosing the best of the current and the new model, and the only way the adversarial peer can "succeed" is by ensuring that the new model post-aggregation is better than the current model(s) already implemented on the devices, which is not exactly a win for any malicious peer intent on derailing the learning process, and if an aggregated model happens to be way off the rails due to adversarial interference and rejected by a majority of the peers, it shall be rejected entirely and the most recent accepted common aggregated model shall be agreed upon to continue training from the next round onwards. (Note that this shall work especially well on P2P networks with defences against Sybil attacks.) 

Results of Decentralised P2P Fed Learning
  Accuracy of Shared Global Model Max Accuracy in Sample Min Accuracy in Sample Mean Accuracy in Sample
Round 1 (Initial) 93.79% 93.84% 92.67% 93.49%
Round 2 94.25% 94.31% 92.77% 94.02%
Round 3 94.75% 94.82% 93.97% 94.48%
Round 4 94.71% 94.99% 93.80% 94.62%
Round 5 94.87% 94.98% 94.38% 94.76%
Round 6 94.97% 95.09% 94.25% 94.85%
Round 7 94.92% 95.14% 93.80% 94.90%

And here's a supporting graph to better visualise these values. Note that the max, min and mean accuracies in the sample refer to those within the subcollection of peers that have participated in a given round. Of interest are the trends of shared global model accuracy (which approaches the baseline vanilla FedAvg accuracy) and the mean cluster/sample accuracy.

So what do we see here? That there seems to be an overall upward trend across the board for all these different statistics, which seems to perfectly suit the end goal of training using federated learning without a server. Also, we can see that even if a peer had not participated in training for a few rounds when it does go for training, it attains accuracy comparable to its other peers in the sample with accuracy (most probably) higher than that for the preceding rounds. (This is not very surprising of course, but it is a desirable property to possess.)

Some Concerns

  • A large proportion of peers must ideally agree for a round of communication, and there might be rounds wherein not a lot of peers would agree. Form of round scheduling might help in this regard, perhaps.

  • Outliers may cause problems. (This is true for vanilla FedAvg anyway, so is not an exclusive concern to this model.)

  • Inter-peer bandwidth could be a bottleneck in P2P networks, so we would do well to reduce communication size somehow (and as mentioned earlier, this can be achieved by the use of a number of well known communication overhead reducing techniques).

  • What about a malicious peer reporting incorrect weights? That’s solved; inaccurate models thus aggregated are rejected by peers, as emphasised earlier. Ideally, one would also want to find a way to either isolate, reduce the influence of or entirely remove the malicious peer. (viz. by a multiplicative weights approach, a peer could reduce a weight corresponding to a peer's reputation whenever it ends up with a less accurate model than the one it already has, and as a result, either decrease the weight accorded to the weight vectors of peers in the subcollection of peers in that communication round or call these peers less often; this is an open line of inquiry at the moment.)

Serving Suggestions (a.k.a. Possible Augmentations to consider while implementing practically)

  • For the security of communication, we can use something like hybrid encryption to encrypt weight vectors in transit (to protect against eavesdropping adversaries, including non-peers).

  • For increasing privacy, differentially private noise can be added.

III. Subclustering of Clients w.r.t. their Local Updates and Creation of Specific Models for Minority Clusters

In general FL techniques create a common model useful for the majority of devices, suffices for most purposes, but in this process, any minor clusters of devices having different data (and ergo producing different weight vectors post local training) than most may benefit from getting more specific models appropriate for their data in certain contexts.

Algorithm:

  • We start with a regular FL (viz. Vanilla FedAvg) approach to training an FL model.

  • Local models of all the devices are clustered (using DB-SCAN) based on their weight vectors.

  • All the devices having the same cluster-id are extracted, and federated averaging is done only for those devices (in a P2P manner). This process is repeated until a model is formed for every cluster.

  • These weights are returned to the server to provide a model for devices having a different and smaller class of dataset. Devices may opt to use the general model or the specific model, if any.

Note about Baselines and an Augmentation we Made

Some background on our (admittedly unorthodox) method of creating this model: one of us had actually conceived this while brainstorming all that we could get up to whilst cooking up and testing new models, and we implemented it to see whether it runs properly on simulated data (created in a way so that there are indeed minority classes devices that have similar data but are different in comparison to most other devices). Post that, we proceeded to look at models that might have a similar approach.

Most baseline algorithms that we saw during our literature review suggested that most of the work that resembled this vein of thought was implemented by clustering devices based on their data itself in some fashion. We on the other hand chose to cluster devices based on the similarity between the local weights produced after local training during each round. (An honourable mention of such a baseline approach that the instructor pointed out would be FLaPS by Paul et al which one of the authors had gone through in the past but did not recall when the other author actually came up with this approach.)

Unfortunately, at a much later stage, it seemed that there was indeed a similar work (with respect to an older version of our model) done by researchers at Keele University, UK (Briggs et al.) with minor differences from our initial model.

So we went ahead and explored adding a P2P component to intra-silo (i.e. within each minority class/cluster) training of specific models, which would endow an additional benefit in terms of each silo getting to keep their weights private; now this would not matter when the server is aware of the clustering pattern as it can easily compute the specific models, but let's say that a group of clients (say they belong to the same organisation/lab) opt to define (among themselves only, assuming they are all connected as peers) a cluster of their own, regardless of the cluster they have been accorded in that round, then given that the server is not made aware of that custom-defined silo/cluster, the specific model would stay private to the members of the cluster.

In short, this augmentation allows clients flexibility to define their own clusters, even if that mightt not give them optimal accuracy.

Experimental Results (with P2P Intra Silo Learning Implemented)

Total number of devices: 125

Number of federated learning rounds(T): 10

Client Sampling Rate (per round): 0.25

Results of Subclustered FL
    Average Testing Error
  No. of Devices For Global Model For Cluster Specific Models
Majority Cluster 110 \(\approx\)0.00203 \(\approx\) 6.71926 \(\times 10^{-15}\)
Minority Cluster 1 8 \(\approx\)0.15474 \(\approx\) 6.30220 \(\times 10^{-13}\)
Minority Cluster 2 7 \(\approx\)0.12130 \(\approx\) 6.59985 \(\times 10^{-16}\)

This goes on to show that for non-IID data or situations with clients that have different data could do well to utilise subclustering like this to obtain well-performing specific models. 

We have only conducted testing for the clusters obtained via DB SCAN on the weight vectors using the older framework (as we ran into time constraints and issues involving implementing DB SCAN on the (even flattened) weights of NNs produced using Keras.

Note that we focused more on simulating these clusters in essence in that older framework, and the code would look more general in real-life use cases (in fact the not-successful code on the DNN/MNIST framework should be general in the abovementioned sense and closer to possible real-life implementations of this.)

(Accuracy on custom-defined clusters has not been tested for given time constraints and that it is an option to be opted for at the clients' discretion and risk. Though given the errors on the global model be, one can expect errors to that tune or even less.)

Possible Future Improvement(s)

Code Links (for the Final Presentation's Material/Models):

Final Presentation Slides

(Kindly Exclude The Title and Bibliography Slides from the Slide Count)

Some Additional References for the Final Presentation

(In addition to the ones already mentioned in prior presentations.)
  1. Monik Raj Behera et al. Federated Learning using Peer-to-peer Network for Decentralized Orchestration of Model Weights. Mar. 2021.
  2. Li Chou et al. “Efficient and Less Centralized Federated Learning”. In: CoRR abs/2106.06627 (2021).
  3. Abhijit Guha Roy et al. “BrainTorrent: A Peer-to-Peer Environment for Decentralized Federated Learning”. In: CoRR abs/1905.06731 (2019).
  4. Shaoxiong Ji et al. “Dynamic Sampling and Selective Masking for Communication-Efficient Federated Learning”. In: CoRR abs/2003.09603 (2020).
  5. Christodoulos Pappas et al. “IPLS : A Framework for Decentralized Federated Learning”. In: CoRR abs/2101.01901 (2021).
  6. Briggs, C., Fan, Z., & András, P. (2020). Federated learning with hierarchical clustering of local updates to improve training on non-IID data. 2020 International Joint Conference on Neural Networks (IJCNN), 1-9.
  7. Sattler, F., Müller, K., & Samek, W. (2021). Clustered Federated Learning: Model-Agnostic Distributed Multitask Optimization Under Privacy Constraints. IEEE Transactions on Neural Networks and Learning Systems, 32, 3710-3722.
  8. Kim, Y., Håkim, E.A., Haraldson, J., Eriksson, H., Silva, J.M., & Fischione, C. (2021). Dynamic Clustering in Federated Learning. ICC 2021 - IEEE International Conference on Communications, 1-6.

We would like to take a moment to express our gratitude to Dr. Subhankar Mishra, not to gain any additional brownie points but to give credit where it is due, for urging us to consider working on federated learning for this project in the first place, which made all of this possible, and for his encouragement and guidance in this respect.

And also to the copious amounts of caffeine that fueled this project.