Scopes of computation   |  How to compute   |  Latest update   |  Download   

How to navigate through the related pages?

Kohn-Sham states computed in a SCF or NSCF calculation are our primary input.

1. The page on Scopes of computation lists all the different calculations performed by our codes.
Itemized links to each scope which opens a page listing related input variables (almost).
The item number(for example 5a) is maintained across all pages for details related to the particular scope.
For example 5a relates to postprocessing in the HAWO basis.

2. The page on How to compute details sequence of calculations for each scope.
Sample input files and compilation scripts are available here.

3. Main codes and subroutines for each scope are available in the Download page. (cred: cmgs,csmg@niser)

Below is an introductory text which is not exhaustive but a good outline.

---<<<<><><>>>>---

Introduction

Our implementations are aimed at evolving strategies towards relatively inexpensive yet workably accurate computation of properties of the ground and excited states of experimentally realizable nanostructures made of few 100s to 1000s of atoms as typical in the frontiers of device applications at nanoscale.

We take the well traded tight-binding route to cut down the cost of computation. The key challenge is to adequately account for the nuances of the many-electron interactions within a tight-binding basis. We started with construction of a suitable localized orbitals from first principles to constitute a minimal basis to maximally represent the electronic structure of a given system within as well as beyond the mean-field approximation of the many-electron approximations.

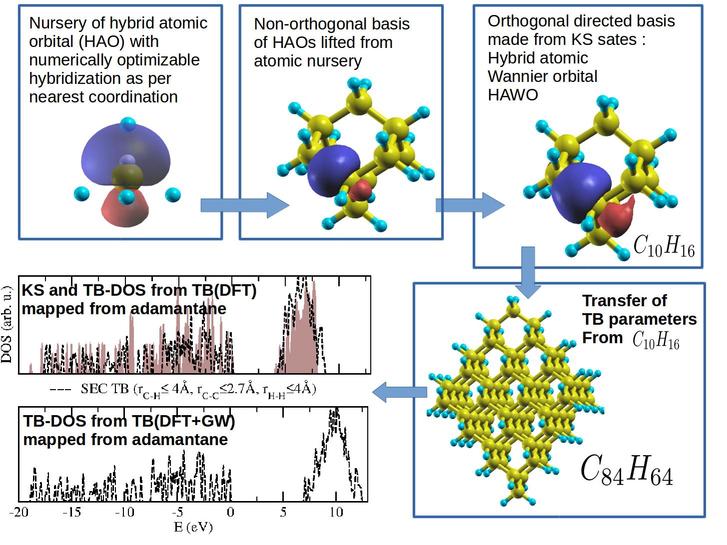
Given a system, the first step of our computation consists of construction of suitable hybrid atomic orbitals from first principles, for the different atoms as per their immediate neighbourhood. Hybrid orbitals are convenient because they can be directed towards directions of coordination, which leads to a sparse Hamiltonian for covalent systems where each nearest neighbour interaction can be represented predominantly by a single off-diagonal element. Locked to the neighbourhood, tight-binding parameters in such a directed basis can be easily transferred across isomorphic systems without bothering about their relative orientations. Directions of coordinations in fully covalent systems, as well as in those with partially covalent nearest neighbour interactions, are predominantly found to follow known coordination polyhedra constituted by selections of s,p,d orbitals as per their symmetry.

For systems with ideal bond-angles, the known degenerate hybrid orbitals naturally orient themselves to the directions of coordination. Although the linear combinations in terms of the pure atomic orbitals leading to the degenerate hybrid orbitals are analytically known, their radial part needs to be consistent with pseudo-potentials in used in order to be well represented in the basis of the Kohn-Sham(KS) states of the given system. Maximal joint diagonalization of the first moment matrices corresponding to the three orthogonal directions is known to render maximally localized Wannier orbitals for isolated systems. We find that the same approach in the basis of KS states of isolated atoms beyond the occupied manifold can render degenerate hybrid orbitals akin to Foster-Boyz localization scheme. The resultant hybrid orbitals thus naturally incorporate the radial dependence decided by the pseudo-potential used.

Subsequent to construction of the hybrid atomic orbitals for individual atoms the orbitals are placed in the given systems with orientation as per the nearest neighbourhoods and Wannierized in the basis of the KS states of the given system. Tight-binding parameters are calculated in the basis of the Wannierized hybrid atomic orbitals using the energies of KS single particle levels, as well as self-energy corrected counterparts calculated using the GW approximations of many-body perturbations theory up to the G0W0 level.

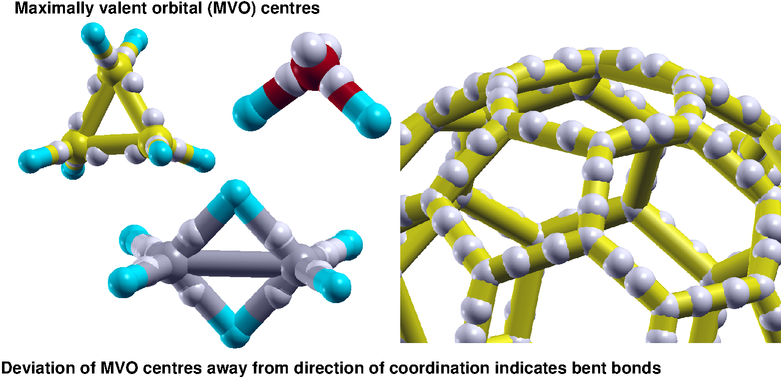
Degenerate hybrid orbitals however can not be used in systems with non-ideal bond angle as we see in many common molecules including water, ammonia etc. For such systems we need to invoke non-degenerate hybrid orbitals and orient them optimally so that they maximally represent covalent interactions prevalent in the system. We have used the Wiberg index, also known as the Mayer bond order, to quantify covalent interaction and chose it as the parameter to optimize the direction of the non-degenerate orbitals. The resultant orbitals have been proposed as maximally valent orbitals which also reveal the bent nature of the path of covalent interaction in systems with non-ideal bond angle.

TB parameters in the directed basis are found to effectively transfer the enhanced correlation resulting from self-energy correction, from smaller reference systems to much larger isomorphic systems, enabling estimation of quasi-particle band-gap of large systems with workable(>90%) accuracy.

We further undertake a host of analysis and computation in the HAWO basis as mentioned in the scope of computation.

---<<<<><><>>>>---